Mateo Gavilanes¹ & Karen Montenegro¹

Escuela de Ciencias de la Tierra, Energía y Ambiente, Yachay Tech University, 100119 Urcuquí, Ecuador

2023

Esta obra está bajo una Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

OBJETIVOS

Los objetivos de este laboratorio son:

• Introducir en algunos métodos estadísticos básicos utilizados en el análisis de riesgos.

PROBLEMA 1

Evaluación de la relatividad de los riesgos.

La siguiente tabla muestra las pérdidas económicas ocasionadas por desastres naturales en varios países.

PERDIDAS ECONÓMICAS TERREMOTOS
AÑO	EVENTO	PAÍS	PERDIDAS (𝟏𝟎𝟗$)
2016	TERREMOTO PEDERNALES	EUADOR	4
2016	TERREMOTO ISLA KYUSHU	JAPON	27,5
2017	TERREMOTO	MEXICO	0,8
2015	TERREMOTO	NEPAL	10
2011	TERREMOTO CHRISTCHURCH	NUEVA ZELANDA	40
2012	TERREMOTO EN EL NORTE DE ITALIA	ITALIA	15,8
2010	TERREMOTO	HAITI	11

a) Calcula las pérdidas económicas como una fracción del producto interior bruto del país (PIB, en inglés Gross Domestic Product, GDP). Ordenar los países en función de la severidad del desastre. Nota: busca en internet los datos de PIB.

PAÍS	AÑO	EVENTO	PERDIDAS (𝟏𝟎𝟗$)	PIB (𝟏𝟎𝟗$)	FRACCIÓN DEL PIB
Ecuador	2016	Terremoto de Pedernales	3.3	98.2	3.36%
Haití	2010	Terremoto de Haití	8.1	6.7	120.90%

PAÍS	AÑO	EVENTO	PERDIDAS (𝟏𝟎𝟗$)	PIB (𝟏𝟎𝟗$)	FRACCIÓN DEL PIB
Italia	2012	Terremotos de Emilia- Romaña	16.0	2073.1	0.77%
Japón	2011	Terremoto y tsunami de Tohoku	210.0	6157.0	3.41%
México	2017	Terremoto de Puebla- Morelos	2.0	1148.0	0.17%
Nueva Zelanda	2011	Terremoto de Christchurch	40.0	171.3	23.36%

Ordenando los países en función de la severidad del desastre, se tiene:

• Haití (120.90%)
  • Nueva Zelanda (23.36%)
  • Ecuador (3.36%)
  • Japón (3.41%)
  • Italia (0.77%)
  • México (0.17%)

b) Basado en tu clasificación de la pregunta a), comenta acerca de los retos que tienen diferentes países cuando se recuperan de un desastre natural.

Los países que sufren mayores pérdidas económicas en relación con su PIB tienen más dificultades para recuperarse de un desastre natural, ya que tienen menos recursos disponibles para reconstruir su infraestructura, atender a las víctimas y reactivar su economía.

Los países que sufren menores pérdidas económicas en relación con su PIB tienen más facilidades para recuperarse de un desastre natural, ya que tienen más recursos disponibles para invertir en la prevención, mitigación y respuesta a los riesgos naturales.

Los países que tienen un nivel de desarrollo más alto también tienen más capacidad para enfrentar los desastres naturales, ya que cuentan con sistemas de alerta temprana, planes de contingencia, normas de construcción sismorresistente y mecanismos de cooperación internacional.

Los países que tienen un nivel de desarrollo más bajo también tienen más vulnerabilidad ante los desastres naturales, ya que carecen de sistemas de protección civil, infraestructura adecuada, servicios básicos y acceso a la ayuda humanitaria.

PROBLEMA 2

Calculo de Riesgo Municipal

La siguiente tabla muestra los costos de recoger la basura después de las fiestas patronales para la ciudad de Ibarra de los últimos 35 años. La ciudad quiere tener un presupuesto razonable para las siguientes fiestas.

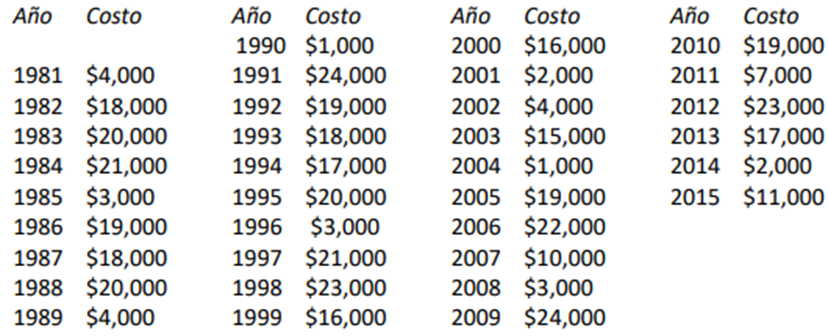
a) ¿Cuál es el promedio (la media de muestra) y cuál es la desviación estándar de los gastos anuales de los últimos 35 años?

Promedio = $13,657.14

Desviación estándar = $8,599.67

b) ¿Asumiendo que los datos tienen una distribución normal, cual es la probabilidad de que Ibarra tenga que gastar $25000 o más para recoger la basura en un año cualquiera?

𝑃(𝑋 ≥ 25,000) = 1 − 𝑃(𝑋 < 25,000)

𝑃(𝑋 ≥ 25,000) = 0.0997

Esto significa que hay un 9.97% de probabilidad de que Ibarra tenga que gastar $25,000 o más para recoger la basura en un año cualquiera.

c) La Contadora del pueblo cree que debe haber algo poco creíble en el estimado de b). Ella tiene razón. ¿Cuál es el problema? [Esta no es una pregunta cuantitativa, y no hay una sola respuesta correcta]

La Contadora del pueblo tiene razón en dudar del estimado de b), porque hay un problema con el supuesto de que los datos tienen una distribución normal. Si se observa la tabla, se puede ver que hay algunos años con gastos muy altos y otros con gastos muy bajos, lo que indica que hay una gran variabilidad en los datos. Además, si se grafica un histograma de los datos, se puede ver que no tienen una forma simétrica y acampanada, sino que tienen una forma sesgada hacia la derecha. Esto significa que los datos no siguen una distribución normal, sino que tienen una distribución asimétrica con una cola larga hacia la derecha. Por lo tanto, no es adecuado usar la fórmula de la distribución normal para calcular la probabilidad de b), ya que puede subestimar o sobreestimar el riesgo real.

Visitas: 0