Mateo Gavilanes¹

Escuela de Ciencias Biológicas e Ingeniería, Laboratorio de Biología 1, Yachay Tech University, 100119 Urcuquí, Ecuador

2023

Palabras claves: Fuerza centrífuga, torque, aceleración, movimiento circular

Resumen  Las leyes de Newton son imprescindibles para describir la dinámica de un movimiento, además su aplicación es sencilla en sistemas inerciales; sin embargo, ¿Qué sucede cuando al movimiento se lo describe desde un sistema de referencia no inercial? Por ello, la presente práctica tiene como objetivo demostrar la existencia de fuerzas ficticias como constructo ideológico, mediante la realización de un sistema que ilustre el accionar de la fuerza centrífuga para justificar la ausencia de aceleración de un objeto en uno de estos sistemas, así como el aumento del radio en proporción de esta. Por otro lado, también se recurrió a determinar la magnitud necesaria de las fuerzas en cada extremo de cuerpo rígido, mediante el ensamblaje de un sistema con pesos variables, con la finalidad de lograr la nulidad en la magnitud del torque. Gracias a esta práctica se logrará comprender la dinámica circular en sistemas no inerciales, así como la manifestación de fuerzas ficticias.

Keywords: Centrifugal force, torque, acceleration, circular motion

Abstract Newton’s laws are essential to describe the dynamics of a movement, and their application is simple in inertial systems; However, what happens when the movement is described from a non-inertial reference system? Therefore, the objective of this practice is to demonstrate the existence of fictitious forces as an ideological construct, by creating a system that illustrates the action of centrifugal force to justify the absence of acceleration of an object in one of these systems, as well as the increase of the radius in proportion to this. On the other hand, the necessary magnitude of the forces at each end of the rigid body was also determined by assembling a system with variable weights, to achieve nullity in the magnitude of the torque. Thanks to this practice, it will be possible to understand circular dynamics in non-inertial systems, as well as the manifestation of fictitious forces.

Introducción

Constantemente se percibe el girar de las manecillas del reloj, o las frenéticas ruedas de los coches, incluso el movimiento de la Tierra cuando se lo aprecia con detenimiento, pero ¿Qué movimiento describe tales situaciones cotidianas?

 Se denomina movimiento circular aquel en el que el cuerpo realiza una trayectoria curvilínea; sin embargo, este puede manifestar una rapidez constante o que varía en cada instante de tiempo [1]. Es por ello, que se denomina movimiento circular uniforme cuando la magnitud de la velocidad es la misma en una trayectoria circular, aunque no implica que la dirección del vector velocidad sea igual en todos los puntos de la circunferencia, debido a que su naturaleza lo impide y solo coincide en una trayectoria rectilínea.

Por otro lado, la cualidad de ‘’uniforme’’ del movimiento circular no descarta que haya aceleración, en vista de que existe una del tipo normal o centrípeta, resultado del cambio de dirección en el vector velocidad y la acción de la fuerza centrípeta. Esta aceleración apunta al centro y es la única que experimentará el MCU (1).

Cabe recalcar que el vector aceleración centrípeta es contante en magnitud, no obstante, cambia su dirección a lo largo de la trayectoria a pesar de apuntar al centro [2]. En cambio, cuando la partícula se mueve cuando la magnitud de  varía al igual que su dirección, aparece una componente tangencial de la aceleración (2) asociado a la trayectoria que es diferente conforme la velocidad también lo sea  [3].

Una vez entendido a grandes rasgos el movimiento circular, para entender su dinámica se considera a un sistema inercial, es decir, aquel »ideal» en donde no interaccionan las fuerzas vecinas, aunque en la naturaleza no existe tal aseveración, pero se puede considerar a las interacciones débiles como despreciables [4]. Dicho esto, para analizar con claridad, se considera que para este tipo de sistemas se requiere la aplicación de las leyes de Newton; notando así que, para producir el movimiento curvilíneo, la fuerza tangencial y fuerza centrípeta (3) son el resultado de la descomposición de  en sus componentes tangencial y radial, de hecho, esta última fuerza es la responsable de mantener el movimiento circular porque en su ausencia, no describiría esa trayectoria [5].

Un ejemplo del accionar de la fuerza centrípeta es la atracción gravitatoria de la Tierra hacia la Luna. Sin embargo, para situaciones de la vida diaria en la Tierra, como el experimento de la presente práctica, se toma en cuenta un sistema de referencia no inercial, es decir, aquel que se mueva rotacionalmente con el planeta, ya que el mismo al ser analizado en base a un sistema inercial, presenta varias aceleraciones distintas como consecuencia de la complejidad de la Tierra desde dicho sistema [4]. Asimismo, para comprender un movimiento desde el punto de vista no inercial, también se necesita de las Leyes de Newton, pero se añade el estudio de fuerzas ficticias -ma0 (fuerzas misteriosas presentes en sistemas no inerciales) para describir correctamente las ecuaciones de movimiento aplicadas. De este modo, aparece la fuerza centrífuga, una de estas fuerzas «extrañas» que es notada cuando un sistema del tipo no inercial está en rotación. Esta fuerza es hacia afuera, contraria a la centrípeta que es en dirección al centro, y perpendicular al radio.

Lo curioso de esta fuerza es que no tiene una existencia real, pero es necesario para explicar el porqué de la nulidad de aceleración en un cuerpo que se encuentra en este tipo de sistema [4].

Igualmente, para simplificar el análisis de un cuerpo en rotación, se puede considerar al sistema de partículas como un cuerpo rígido o, en otras palabras, como un todo en donde las partículas que lo integran no vibran y mantienen una posición fija ante las fuerzas externas (no se deforman), entonces de esta manera se analiza el accionar de una fuerza en un objeto en donde la deformación es depreciable. En vista de lo antes mencionado, surge el torque; una magnitud física que mide el movimiento rotacional, el cual es producto de la aplicación de una fuerza en algún punto de un cuerpo rígido. La magnitud del torque viene dada por la fórmula (4), en donde α es el ángulo entre la fuerza aplicada (F) y su posición (r) [6]. Es importante acotar que se considera al torque positivo si la rotación que produce la fuerza es en sentido antihorario y negativo si es antihorario.

Metodología

La cuantificación y la descripción de las fuerzas involucradas en el movimiento de una partícula son esenciales en dinámica rotacional, por lo que en la presente práctica se han planificado y llevado a cabo las siguientes actividades para evaluar en varios diagramas de cuerpo libre el papel de una fuerza específica en el denominado movimiento de torque y la denotación de las fuerzas involucradas, tales como, centrípeta, normal y tangencial.

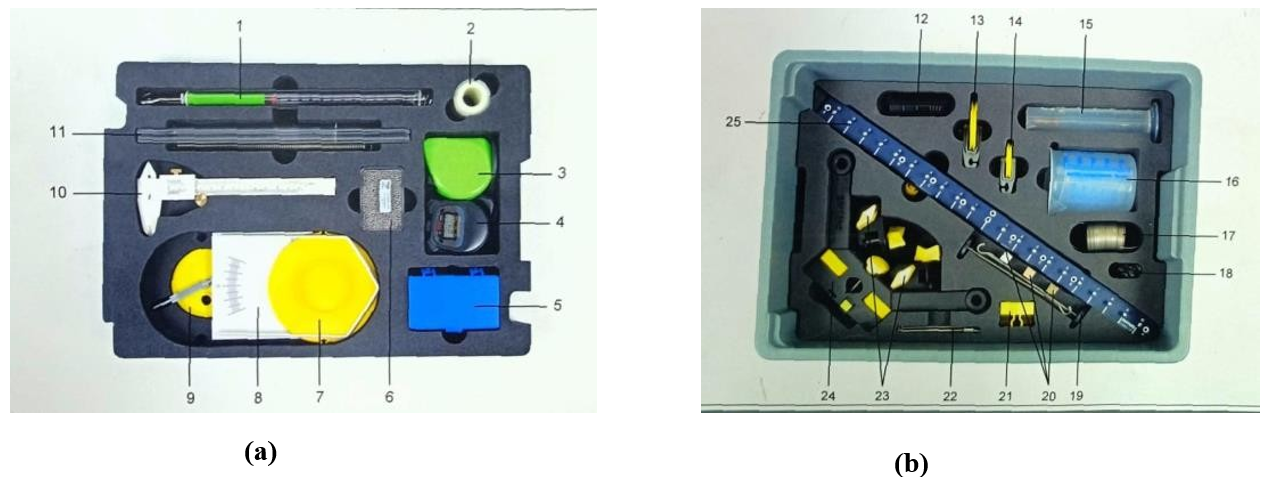
De esta manera, el Set Mecánico de Física de Phywe, que contiene 25 elementos e instrumentos de medida, sirvió como base para desarrollar los experimentos previstos (Figura 1). Para la elaboración de la experiencia 1 se armó una estructura con las varillas de soporte (a), un soporte de base variable (b), nueces para asegurar(b) y un soporte base (b). Para la experiencia 2 se utilizaron materiales externos a la figura 1 ya que este ya estaba previamente preparado por la maestra, los materiales que se usaron fue una base giratoria con distinción del radio, un carrito con soporte de masa variable, hilo para pescar (a), máquina que proporcionaba la fuerza para generar la rotación de la base, un timer centrado en la posición de la base giratoria, un flexómetro de 0,2 N, una pinza de anclaje de este y un sistema de poleas conectado al carro y al dinamómetro.

2.1 Actividad 1. torques

La base de soporte de base variable con la regleta ajustable fue variando en diferentes posiciones su masa y su equilibrio, se realizaron 10 intentos en los cuales se fueron cambiando las posiciones de puntos de equilibrio de la regleta y para ajustar el desbalance, para el cual se eligieron aleatoria.

Los datos obtenidos se evaluarán en la tabla 1 considerando el desequilibrio y la igualación con las masas hasta que la medida graduada sea nula y este en completo equilibrio. En definitiva, esta actividad tiene como finalidad evaluar momento de torque y su relación con el peso del teniendo en cuenta la variación de posición y el desbalance del sistema. (Figura 2)

2.2  Movimiento circular (fuerza centrífuga)

La configuración experimental que se visualiza en la Figura 3, esta distribuida de manera que el indicador rojo suministrado debe colocarse en la barra central del automóvil indicando la distancia del eje de rotación (radio). En el extremo externo del aparato centrífugo, una cuerda es pegada entre las barras de guía y sirve de arranque y parada de la barrera de luz.

Al medir la duración de un interruptor de ciclo completo a modo que cada vuelta tendrá un tiempo definido y este deberá de ser constante. En esta sección del experimento, la masa del automóvil se mantiene constante, al igual que un radio, en presencia de diferentes velocidades angulares. Como en la sección 1, el carro de medición se lleva a la posición r. Empujando el carro desde el interior hacia el exterior (Figura 3).

Resultados

Para finalizar las actividades se tienen las siguientes observaciones y resultados.

Actividad 1

Sistema	Masa 1 (kg)	Masa 2 (kg)	(m)	(m)	Equilibrio (Si / No)	(N)	(N)	(Nm)	(Nm)	Sumatoria
1	0,13	0,15	0,144	0,126	SI	1,274	1,47	0,183	-0,185	-0,02
2	0,10	0,21	0,161	0,83	SI	0,98	2,058	0,158	-0,171	-0,013
3	0,10	0,30	0,179	0,6	SI	0,98	2,94	0,176	-0,176	0
4	0,10	0,14	0,141	0,102	SI	0,98	1,372	0,138	-0.14	-0,002
5	0,10	0,18	0,180	0,82	NO	0,98	1,764	0,176	.0,145	0,031
6	0,20	0,12	0,121	0,20	SI	1,96	1,176	0,237	-0,235	0,002
7	0,46	0,10	0,43	0,179	SI	4,508	0,98	0,194	-0,176	0,018
8	0,11	0,15	0,142	0,102	NO	1,078	1,47	0,153	-0.15	0,003
9	0,17	0,42	0,202	0,83	NO	1,666	4,116	0,337	-0,342	-0,005
10	0,10	0,15	0,62	0,42	SI	0,98	1,47	0,061	-0,062	-0,001

La sumatoria de torques es igual a cero cuando el cuerpo rígido está en equilibrio rotacional. Esto se debe a que, en equilibrio rotacional, la fuerza neta que actúa sobre el cuerpo es cero. En consecuencia, la sumatoria de torques también debe ser cero. [1]

Se utilizó un sistema de soporte de masas variables para estudiar el equilibrio rotacional. Al variar los pesos de las masas y el cambio al peso y radio con respecto al centro, se pudo observar que la sumatoria de torques era igual a cero cuando el sistema se encontraba en equilibrio. Este comportamiento es consistente con lo que se predice por la teoría. Según la segunda ley de Newton, la fuerza neta que actúa sobre un cuerpo es igual a la masa del cuerpo multiplicada por su aceleración. En el caso de un cuerpo rígido en equilibrio rotacional, la aceleración es cero. Por lo tanto, la fuerza neta también es cero. [1,2]

Las radios de las poleas tienen una influencia directa en el equilibrio rotacional del sistema. En general, cuanto mayor sea el radio, menor será el torque que se necesita para producir la misma rotación. En la práctica, se supervisa que, al aumentar la radio de una polea, se necesita una masa menor para poner el sistema en equilibrio. Esto se debe a que el brazo de palanca de la fuerza producida por la masa es mayor. [2]

Actividad 2

No.	Masa (Kg)	t (s)	vtang (m/s)	Fuerza centrífuga (N)	Radio (m)	W (rad/s)
1	0.05	0,070	0,064	0,06	0,145	0,441
2	0.07	0,070	0,064	0,08	0,145	0,441
3	0.09	0,070	0,064	0,09	0,145	0,441
4	0.1	0,070	0,064	0,1	0,145	0,441
5	0.12	0,070	0,064	0,14	0,145	0,441

En esta tabla, se mantiene constante la radio y la velocidad angular de las masas, pero se varía la masa de estas. Al aumentar la masa de las masas, se observa que aumenta la fuerza centrífuga, que es la fuerza que actúa sobre las masas para mantenerlas en movimiento circular. Esto se debe a que la fuerza centrífuga es proporcional a la masa de las masas. También se observa que aumenta la tensión en las cuerdas, que es la fuerza que se ejerce sobre las cuerdas para mantener las tensas. Esto se debe a que la tensión es proporcional a la fuerza centrífuga [1,2].

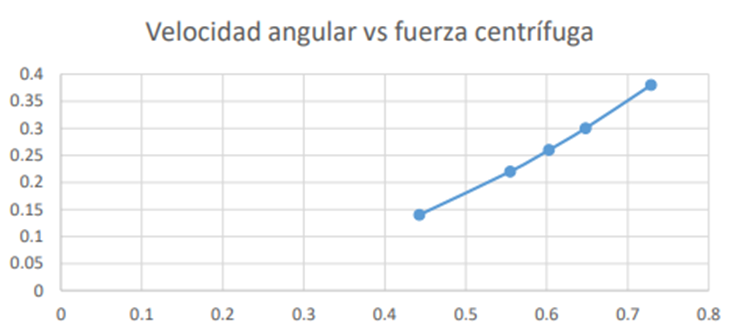
La razón por la que la gráfica es una línea recta es que la fuerza centrífuga es proporcional a la masa del objeto. A medida que la masa aumenta, la fuerza centrífuga también aumenta. Esto se debe a que la fuerza centrífuga es la fuerza que actúa sobre un objeto que se está girando. Esta fuerza es proporcional a la masa del objeto y a la velocidad angular del objeto. En este caso, la velocidad angular del objeto es constante, por lo que la fuerza centrífuga es proporcional a la masa del objeto.

De esta manera, podemos concluir que la gráfica de fuerza centrífuga en función de la masa es una línea recta, con una pendiente igual a la constante de proporcionalidad entre las dos variables.

No.	Masa (Kg)	t (s)	Vtang (m/s)	Fuerza centrífuga (N)	Radio (m)	W (rad/s)
1	0,12	0,06	0,12	0,2	0,145	0,993
2	0,12	0,054	0,15	0,24	0,145	1,051
3	0,12	0,051	0,16	0,28	0,145	1,082
4	0,12	0,047	0,17	0,32	0,145	1,113
5	0,12	0,044	0,18	0,38	0,145	1,144

Aquí se mantiene constante la masa de las masas, pero se varía la velocidad angular de las mismas. Al aumentar la velocidad angular de las masas, se observa que aumenta la fuerza centrífuga, que es la fuerza que actúa sobre las masas para mantenerlas en movimiento circular. Esto se debe a que la fuerza centrífuga es proporcional al cuadrado de la velocidad angular. [1]

También se observa que aumenta la tensión en las cuerdas, que es la fuerza que se ejerce sobre las cuerdas para mantener las tensas. Esto se debe a que la tensión es proporcional a la fuerza centrífuga.

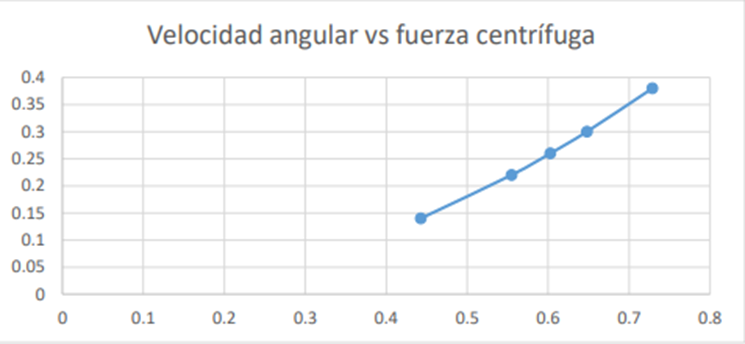
Como se puede ver, la gráfica es una línea recta, lo que indica que existe una relación lineal entre las dos variables. La pendiente de la línea es igual a la constante de proporcionalidad entre la fuerza centrífuga y la velocidad angular al cuadrado. En este caso, la pendiente es de 0,25.

La ecuación de la relación entre la fuerza centrífuga y la velocidad angular al cuadrado es la siguiente:

No.	Masa (Kg)	t (s)	Vtang (m/s)	Fuerza centrífuga (N)	Radio (m)	W (rad/s)
1	0,120	0,070	0,77	0,16	0,172	89,6
2	0,120	0,070	0,79	0,18	0,177	89,6
3	0,120	0,070	0,86	0,19	0,194	89,6
4	0,120	0,070	0,92	0,20	0,206	89,6
5	0,120	0,070	0,98	0,22	0,221	89,6

Podemos observar que se mantiene constante la masa de las masas y la velocidad angular de las mismas, pero se varía el radio de las poleas.

Al aumentar el radio de las poleas, se observa que disminuye la fuerza centrífuga, que es la fuerza que actúa sobre las masas para mantenerlas en movimiento circular. Esto se debe a que la fuerza centrífuga es inversamente proporcional al radio de las poleas. También se denota que disminuye la tensión en las cuerdas, que es la fuerza que se ejerce sobre las cuerdas para mantener las tensas. Esto se debe a que la tensión es inversamente proporcional al radio de las poleas. [1,2]

En general, se observa que, al aumentar la masa de las masas, la velocidad angular o el radio de las poleas, aumenta la fuerza centrífuga y la tensión en las cuerdas. Estos resultados son consistentes con las leyes del movimiento circular uniforme y uniformemente variado.

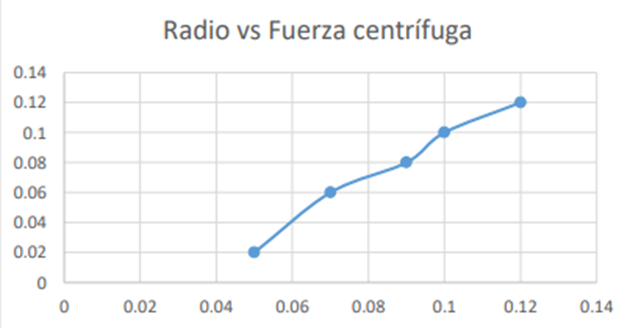
Como se puede ver, la gráfica es una línea recta, lo que indica que existe una relación lineal entre las dos variables. La pendiente de la línea es igual a la constante de proporcionalidad entre la fuerza centrífuga y la radio. En este caso, la pendiente es de 0,04.

Otra razón es ya que tiene relación la fuerza centrífuga es proporcional al producto de la masa del objeto, la velocidad angular del objeto y el radio del círculo. En este caso, la masa y la velocidad angular son constantes, por lo que la fuerza centrífuga es proporcional al radio del círculo.

Este comportamiento es consistente con la ecuación de la fuerza centrífuga, que se puede escribir de la siguiente manera:

Fc = mω^2r

Tras examinar las medidas de cada experimento, se ha observado lo siguiente:

En sistemas en equilibrio y de medición de torques, se ha observado que se produce un torque más grande cuando se considera un mayor peso (fuerza aplicada) y una mayor distancia entre el centro de rotación y la línea de acción de la fuerza.

En un sistema que gira con radio y tiempo constante. La Tabla 2 muestra que una mayor masa aumenta la velocidad tangencial y angular, lo que significa que la relación es directamente proporcional.

Sin embargo, en un sistema rotacional con masa constante, radio constante y velocidad variable, la relación entre la velocidad angular, tangencial y la fuerza centrípeta es directamente proporcional y inversamente proporcional al tiempo.

Finalmente, un sistema rotacional con masa, tiempo constante y radio variable, aunque puede haber un margen de error, nos muestra un aumento significativo en la velocidad angular y tangencial a medida que aumentamos el radio y la fuerza centrípeta.

Por lo tanto, estos hallazgos son cohesivos y cumplen con los principios fundamentales de la mecánica y el movimiento rotacional.

Conclusiones

Sintetizar brevemente los puntos más relevantes, aportando los conocimientos explorados a lo largo del texto, pero teniendo el cuidado de no repetir exactamente lo que ya has escrito (¡evita la redundancia!), ni de anexar una nueva información que no se haya mencionado antes.

Referencias

1. R. a. Serway and L. D. Kirkpatrick, Física para ciencias e ingeniería, vol. 1, no. 7. 2008.
2. R. Resnick, D. Halliday, and K. Krane, Fisica 1 Y 2. 2001.
3. R. a. Serway and L. D. Kirkpatrick, Física para ciencias e ingeniería, vol. 1, no. 7. 2008.
4. M. R. Ortega Girón, “Lecciones de física,” Monografías y textos, 2006.
5. M. Alonso and E. Finn, “Física Vol. I, Mecánica,” Wilmington, Delaware, EUA, Addison Wesley Iberoamericana, pags, vol. 8, 1986.
6. Juan Inzunza B., Física: introducción a la mecánica, vol. 311. Concepción, Chile, 2002.

Visitas: 1