Movimiento Armónico Simple

Isaac Mateo Gavilanes Chávez & Ethan Aaron Guevara López

Universidad de Investigación Experimental Yachay Tech, Escuela de Ciencias Físicas y Nanotecnología. Urcuquí, Ecuador. (2024).
Isaac.gavilanes@yachaytech.edu.ec
Ethan.guevara@yachaytech.edu.ec

Resumen
Una práctica para estudiar los movimientos armónicos simples (MAS) se llevó a cabo en el laboratorio de oscilaciones. El objetivo principal fue analizar y mostrar cómo la amplitud y la fase inicial afectan la frecuencia y el comportamiento general del MAS. Se diseñaron dos experimentos: uno con un péndulo simple y otro con un sistema de masa-resorte. La fase inicial, la amplitud y la frecuencia de las oscilaciones se midieron en ambos casos. Se modificó la longitud de la cuerda para el péndulo y la masa suspendida del resorte. Los resultados demostraron que la frecuencia del MAS tanto para el péndulo como para el resorte es inversamente proporcional a la raíz cuadrada de la amplitud. También se descubrió que la fase inicial establece el punto de inicio del movimiento oscilatorio. Por último, pero no menos importante, esta práctica de laboratorio permitió comprender y mostrar las características del MAS. Se confirmó que la amplitud determina la frecuencia del MAS y que la fase inicial determina la posición inicial del movimiento. Los hallazgos confirman la teoría y brindan una base sólida para el estudio de sistemas oscilatorios más complejos.

Abstract
A practice to study simple harmonic motions (MAS) was carried out in the oscillation laboratory. The main objective was to analyze and show how amplitude and initial phase affect the frequency and overall behavior of MAS. Two experiments were designed: one with a simple pendulum and the other with a mass-spring system. The initial phase, amplitude and frequency of the oscillations were measured in both cases. The length of the rope for the pendulum and the suspended mass of the spring were modified. The results showed that the frequency of MAS for both the pendulum and the spring is inversely proportional to the square root of the amplitude. It was also found that the initial phase establishes the starting point of the oscillatory movement. Finally, this laboratory practice made it possible to understand and show the characteristics of MAS. It was confirmed that amplitude determines the frequency of MAS and that the initial phase determines the initial position of the movement. The findings confirm the theory and provide a solid foundation for the study of more complex oscillatory systems.

Introducción

El estudio de las oscilaciones es un tema fundamental en muchos fenómenos naturales y sistemas tecnológicos, dentro del campo de la física. Es fundamental comprender las oscilaciones para entender el comportamiento del universo, desde las vibraciones de átomos en moléculas hasta el movimiento de planetas en órbitas elípticas. Las oscilaciones son movimientos repetitivos que se producen en un sistema alrededor de una posición de equilibrio. Estas ondas se derivan de la ecuación diferencia de segundo orden a partir de la segunda ley de Newton y la ley de Hooke, para el análisis de fuerzas y energías en el caso de un resorte. La ley de Hooke establece que la fuerza restauradora ejercida por un resorte es proporcional al desplazamiento del resorte desde su posición de equilibrio[1], [2]:

F = −kx (1)
Donde F es la fuerza, k una constante elástica del resorte y X representa al vector desplazamiento desde una posición de equilibrio.

La segunda ley de Newton establece que la fuerza es igual a la masa por la aceleración:

F = ma (2)

Al igualar ambas expresiones para una fuerza F, dividendo ambos lados por m y considerando que la aceleración es la segunda derivada del desplazamiento con respecto al tiempo, se obtiene la ecuación diferencial que describe a las oscilaciones, que es la siguiente:

Dentro de dicho contexto el movimiento armónico simple o abreviado como MAS, se lo describe y estudia como una solución particular que satisface a la ecuación diferencia que describe a una oscilación. En este caso se produce cuando existe una fuerza que actúa sobre un objeto es proporcional y opuesta al desplazamiento del objeto desde su posición de equilibrio de un objeto alrededor de un punto de equilibrio[3], [4], la ecuación característica del MAS es:

x(t) = Acos(𝜔𝑡 + 𝜙) (4)

Los parámetros 𝐴, 𝜔, y 𝜙 son constantes del movimiento. Donde 𝐴, es la llamada amplitud del movimiento, es simplemente el máximo valor de la posición de la partícula en la dirección 𝑥 positiva o negativa. La constante 𝜔 se llama frecuencia angular y tiene unidades 𝑟𝑎𝑑/s. Es una medida de qué tan rápido se presentan las oscilaciones; mientras más oscilaciones por unidad de tiempo haya, más alto es el valor de 𝜔 y a partir de las ecuaciones de movimiento circular uniforme (mcu) se sabe que 𝜔:

Donde m representa la masa del resorte.

Para la practicidad del estudio de los osciladores armónicos, al considerar que su estudio es en un sistema ideal, el ángulo de desfase inicial se desprecia, pues se estudia a las ondas cuando estas llegan a una posición máxima x=A, por tanto 𝜔 = 0[4], [5]. Debido a que se deprecio una incógnita lo único que queda hallar es el periodo, pero por mcu se sabe que

Donde la frecuencia 𝑓 oscilación y está dada en Hz.

Del mismo modo que una las fórmulas de para cualquier movimiento se tendrá que al derivar esta expresión obtendremos en la primera derivada a la velocidad y como segunda derivada la aceleración, que se representan con las siguientes formulas:

Debido a su comportamiento sinusoidal se puede deducir fácilmente que cuando se encuentran en su amplitud máxima, en los ceros y unos de las funciones senos y cosenos, las velocidades serán máximas, quedando que:

Al momento de realizar el análisis de energía de estos osciladores, teóricamente se sabe que se conserva ya que no existen perdidas debido a fuerzas externas como la fricción por lo que la ecuación queda así:

A lo largo de un ciclo completo de oscilación, la energía se intercambia continuamente entre energía cinética y energía potencial, pero la energía total del sistema permanece constante. Esto es una manifestación del principio de conservación de la energía[6], y ya desglosando la expresión y desarrollando la formula de la ley de conservación de energía en función de las ecuaciones (4, 7 y 8) y agrupando términos se reduce y obtiene lo siguiente:

Por otra parte, también existe el péndulo simple, el cual consiste en una masa puntual suspendida de un hilo inextensible sin masa, y cumple que para ángulos pequeños inferiores o iguales a 15°, permiten aproximarse a MAS. La ecuación de este se deriva considerando a las fuerzas involucradas en el movimiento, la fuerza gravitacional sobre la masa m es 𝐹_𝑔 = 𝑚𝑔 donde g es la aceleración debido a la gravitación universal. Esta fuerza tiene componentes tangenciales y radiales al arco de la trayectoria del péndulo, su componente tangencial 𝑚𝑔𝑠𝑖𝑛(𝜃) es la responsable de la aceleración tangencial y, por lo tanto, del movimiento angular. Utilizando la ley de Newton para el movimiento angular, se puede obtener la ecuación diferencial del péndulo simple:

Como se mencionó antes para los ángulos pequeños a menores o iguales a 15, permitiendo aproximaciones del ángulo máximo de oscilación y así a su vez simplificar la misma.

Así pues, para cualquier tiempo t resulta en la siguiente ecuación:

Donde 𝜃_𝑚𝑎𝑥 es el ángulo máximo al cual oscilara el péndulo.

Y la fórmula para poder determinar el periodo dependerá de la longitud de la cuerda:

Existiendo una relación cuadrática proporcional que muestra como el periodo aumenta a medida que la longitud lo hace.

De aquí se sigue el análisis de la energía del sistema, en el cual intervienen la energía potencial gravitatoria y la energía cinética de la siguiente forma:

Donde h es la altura del péndulo.

Al momento de hacer el análisis de fuerzas se sabe que para un ángulo de oscilación máximo 𝜃, la altura será igual a la energía potencial gravitatoria, ya que el péndulo se detiene, y en dicho punto la altura máxima h se puede calcular de la siguiente forma:

ℎ = 𝐿(1 − 𝑐𝑜𝑠(𝜃) (19)

Dejando así que para el caso particular de un ángulo 𝜃 máximo la energía total será la siguiente:

𝐸𝑇 = 𝑚𝑔𝐿(1 − 𝑐𝑜𝑠(𝜃) (20)

Es gracias al entendimiento de todas estas ecuaciones que se buscara en la presente practica de laboratorio se abordarán las hipótesis planteadas en base al conocimiento previo ya expuesto, con el objetivo principal es proporcionar una comprensión más profunda de los principios fundamentales de la física que rigen el movimiento armónico simple y su aplicación en diversos contextos físicos y tecnológicos.

Metodología

Demostrar el movimiento oscilatorio de un sistema para comprender su comportamiento y el cómo interactúan en el infinito cosmos, es por ello por lo que, se realizaron cuatro experiencias para analizar cómo se comporta el movimiento oscilatorio en circunstancias en donde intervienen fuerzas no conservativas y conservativas. De esta manera, se utilizaron elementos de dos Sets Mecánicos de Física de Phywe, que contienen 25 y 15 elementos e instrumentos de medida respectivamente, los mismos que sirvieron como base para desarrollar los experimentos previstos (Figura 1 ). Para la elaboración de la experiencia 1, se armó una estructura con las varillas de soporte (a), un soporte de base variable (b), nueces para asegurar(b) y un soporte base (b), además de añadir un muelle metálico de 3 N/m de constante elástica (b), Resorte helicoidal, 20 N/m, pin de sujeción(a), soporte de tubo de vidrio con almeja de cinta métrica(a)

Actividad 1. Demostración de la ley de Hooke

El soporte de base variable se ajustó con la varilla de 0.3 m para formar una estructura que mantenga fijo al muelle metálico. De esta manera, se tomó la posición inicial (𝑥1) del mismo para ubicar el dato en la Tabla 1, así pues, también se anexó el valor de la altura inicial (ℎ1). Seguidamente, se aplicaron masas de 0.010 kg. 0.020 kg, 0.030 kg, 0.040 kg, 0.050 kg, 0.060 kg y 0.070 kg para evaluar la deformación del resorte, y con ello su constante elástica a partir de datos experimentales (Figura 2). Así mismo se realizaron la misma toma de datos, pero aplicando el otro resorte. Gracias a esta experiencia se podrá conocer más sobre un sistema oscilatorio, además del comportamiento del peso y el muelle.

Actividad 2. Demostración del Péndulo Elástico

Se debe seguir un procedimiento estructurado que garantice la precisión de los resultados para llevar a cabo la práctica del sistema masa-resorte y estudiar sus oscilaciones. Primero, se instala el sistema asegurándose de que el resorte esté fijo en un extremo y la masa suspendida libremente en el otro. Después de instalar el sistema, la masa debe moverse 1 cm de su posición de equilibrio, lo que equivale al 10% de la longitud del resorte en reposo. El inicio de las oscilaciones depende de este desplazamiento inicial.

Posteriormente, se calcula la cantidad de tiempo que tarda el sistema en completar 4 y 8 oscilaciones. El periodo (T), que es el tiempo promedio para una oscilación completa, se puede calcular mediante estas mediciones. Para garantizar la consistencia de los datos, que se detallan detalladamente en la Tabla 2, es crucial repetir este proceso cinco veces. Posteriormente, el experimento se repite con una masa diferente, manteniendo el resorte intacto. La Tabla 2.1 contiene los datos más recientes. Este cambio de masa tiene un impacto en las propiedades oscilatorias del sistema.

Finalmente, se crean gráficos de posición (x(t)), velocidad (v(t)) y aceleración (a(t)) para ambos sistemas de masas utilizando los datos recopilados en las tablas 2.1 y 2.2. Para analizar el comportamiento oscilatorio y verificar los cambios en la frecuencia angular (omega) con diferentes masas, estos gráficos son esenciales. Este análisis gráfico proporciona una comprensión visual del fenómeno estudiado y confirma la teoría.

Actividad 3. Demostración del Péndulo Simple.

Parte A
Se sigue un procedimiento metódico para investigar las propiedades oscilatorias de un péndulo simple, que comienza con la configuración inicial del sistema. Después de elegir una longitud de cuerda (l1 ) y una masa oscilante (m1 ), desplazamos el péndulo desde su posición de equilibrio por un pequeño ángulo que cumpla con la condición de linealidad del péndulo simple, es decir, un ángulo que no exceda los 15°. Antes de permitir que el péndulo se mueva libremente, se registra cuidadosamente este ángulo inicial, así como la masa y la longitud de la cuerda.

Elaboración de un carro de Vapor (Steam Cart)

Procedemos a medir el tiempo que tarda en realizar 4 o 8 oscilaciones completas con el péndulo en movimiento. La Tabla 4 muestra los resultados de estas mediciones, que se han repetido cinco veces para garantizar su precisión. Calculamos el periodo de oscilación (T), que es el tiempo promedio para una oscilación completa, a partir de estos tiempos.

El experimento se realiza de nuevo con una longitud de cuerda (l2) diferente y la misma masa oscilante. Una nueva tabla, similar a la Tabla 5, se crea para registrar los resultados. Con los datos de ambas tablas, se deben crear gráficos de posición (x(t), velocidad (v(t) y aceleración (a(t)) para ambos sistemas, lo que nos permite ver cómo los cambios en la longitud de la cuerda afectan la frecuencia angular (omega). Además, calculamos las energías potenciales y cinéticas para cada tiempo que se muestra en la Tabla 5 utilizando solo la longitud (l1). Este paso es esencial para comprender la conservación de energía en un sistema oscilante.

Parte B

Se incrementa el ángulo de desplazamiento a 60° para la longitud máxima (l2) y la masa utilizada en la Parte A. Esto nos saca de la aproximación de linealidad del péndulo simple. Así mismo, se debe medir el tiempo para 4 y 8 oscilaciones completas, repetimos el proceso cinco veces y registramos los datos en la Tabla Dado que la aproximación lineal ya no es válida y las fuerzas restauradoras no son proporcionales al
desplazamiento, este experimento final nos permite discutir por qué este sistema, con un ángulo tan grande, no puede considerarse un Movimiento Armónico Simple (MAS).

Actividad 4. Uso del generador de funciones

Las características fundamentales de las ondas periódicas son el objetivo de esta actividad de laboratorio. Aquí se tendrá la oportunidad de visualizar y comprender cómo la frecuencia y el voltaje pico afectan la forma de una onda creando ondas senoidales, cuadradas y triangulares. Además, se calculará la frecuencia y el periodo, que son conceptos fundamentales para el estudio de las ondas. Esta experiencia real no solo apoya la teoría aprendida en clase, sino que también establece una base sólida para futuras aplicaciones en física e ingeniería. La capacidad de generar y analizar una variedad de ondas es crucial para el diseño de circuitos electrónicos, así como para comprender la propagación de señales de varias maneras.

Resultados

Actividad 1.
Al cabo de finiquitar las actividades propuestas, se analizó los siguientes resultados obtenidos:

En cuanto a la proporcionalidad, los valores de peso (fuerza) y el cambio en la longitud (∆L) parecen ser directamente proporcionales, lo cual es consistente con la Ley de Hooke. A medida que aumenta la masa (y por lo tanto la fuerza), el cambio en la longitud del recurso también aumenta, siendo directamente influyente con la constante de resorte o la constante de recurso (k) que puede ser calculada para cada masa. Sin embargo, los datos no proporcionan un valor único de (k), lo que podría deberse a errores experimentales o a la no linealidad del material después de cierto límite elástico representando algo muy significativo en su comportamiento elástico.

Hasta cierto punto, el resorte regresa a su longitud original (Lo) cuando se elimina la fuerza, lo que indica un comportamiento elástico. Y para el apartado del análisis de los datos, la variación en los valores de ∆L para las dos series de medidas (Lo1 y Lo2) es relativamente pequeña, lo que sugiere que el experimento se realizó con cierto grado de precisión proporcionando la conclusión de que los datos experimentales apoyan la Ley de Hooke dentro del rango de masas utilizadas. Sin embargo, sería útil realizar más pruebas, especialmente cerca del límite elástico del material, para observar cualquier desviación de la linealidad y para calcular con precisión la constante de resorte del material.

Actividad 2.

Las tablas presentadas muestran los resultados de un experimento para calcular el período de oscilación de un recurso según la Ley de Hooke y su relación con el período de un oscilador armónico simple. La masa suspendida del resorte (m) se representa, la constante del resorte (k) se representa y la elongación del resorte (x). En cuanto a las observaciones experimentales se toma en considera la consistencia cuando se duplica el número de oscilaciones, el tiempo promedio para 4 y 8 oscilaciones se duplica, lo que es esperado. El período (T) de cada masa se puede encontrar dividiendo los promedios de tiempo de cuatro oscilaciones por cuatro o de ocho oscilaciones por ocho. Los valores de (T) obtenidos están cerca de los valores teóricos esperados, lo que indica una buena precisión experimental.

La influencia de la masa: el período de oscilación aumenta al aumentar la masa de m1 a m2, lo que es consistente con la teoría porque un mayor (m) resultará en un mayor (T) si (k) se mantiene constante esto es de manera directa con la precisión de las mediciones con una pequeña variación en los tiempos individuales para un numero específico de oscilaciones indica que las mediciones son precisas y que las variables experimentales están bien controladas, generando las conclusiones de que la teoría del oscilador armónico simple y la Ley de Hooke describen la relación entre la masa, la constante del resorte y el período de oscilación del resorte. Los datos experimentales respaldan esta teoría. La validez de los resultados se refuerza por la consistencia en los tiempos medidos para un número predeterminado de oscilaciones.

Este análisis se basa en los datos proporcionados y asume la precisión de las mediciones, así como la validez de la Ley de Hooke y la teoría del oscilador armónico simple para el rango de masas y constantes de recurso utilizadas. Para confirmar estos hallazgos y explorar el comportamiento en varios rangos de masa y constantes de recurso, se recomienda realizar más experimentos.

Actividad 3.

Tabla 5. Periodos de Oscilación para un Péndulo Simple longitud L2

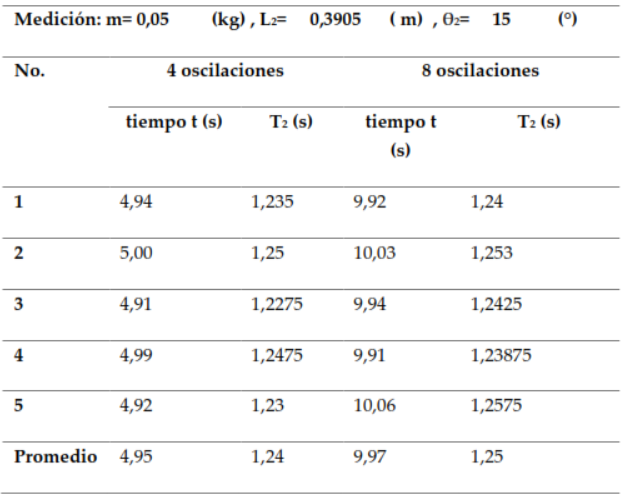
Después de recopilar los datos, se analizaron las tablas que muestran el periodo de oscilación de un péndulo en función de su longitud. Se consideró el ángulo máximo soportable, en el cual las oscilaciones teóricamente se consideran como máximas para este análisis, con el fin de demostrar que la variación del periodo es proporcional a la longitud de la cuerda del péndulo en un Movimiento Armónico Simple (MAS). Según la ecuación (17) del periodo de un péndulo simple, sabemos que el período variará dependiendo de la longitud de la cuerda. Aumentar la longitud L de la cuerda también conlleva a un aumento en el periodo de oscilación T.

La relación es cuadrática, lo que significa que un ligero aumento en la longitud resulta en un incremento proporcionalmente mayor en el periodo, esto se vio al determinar los valores medios de los periodos para 4 y 8 oscilaciones a dos longitudes diferentes: El periodo experimentó un aumento significativo al cambiar de L1 a L2, con longitudes respectivas de 0.332 m y 0.3905 m. Al comparar estos resultados experimentales con el valor teórico del periodo que fue calculado a partir de la ecuación del péndulo simple, se observó que existía una variación de ± 0.5 s para L1 y de ± 1 s para L2 con respecto al valor real. Entonces experimentalmente se demuestran que la relación entre el periodo y la longitud es aproximadamente proporcional a la raíz cuadrada, tal como predice la teoría del péndulo simple.

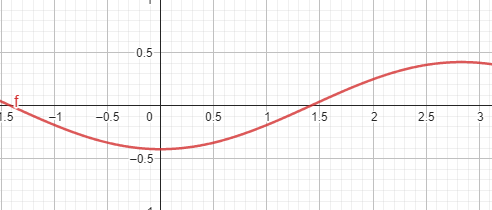
En este apartado, se seleccionó al péndulo con longitud L1 en el periodo de cuatro oscilaciones con un valor de 1.10 s para poder analizar el estudio de la conservación de energía. Con estos datos, se calculó la energía total del sistema utilizando la ecuación de conservación de energía. Para simplificar los cálculos, se estudió la energía total del sistema en un punto máximo de la oscilación, donde la velocidad es cero. En este punto, la energía potencial del sistema es igual a la energía total, ya que toda la energía está en forma de energía potencial. Como la masa del péndulo no cambió durante el experimento, la energía total del sistema se mantuvo constante. Se estudio la variación sinusoidal de las energías cinética y potencial en función del tiempo, causada por el cambio en la posición y ángulo de oscilación θ del péndulo.

Durante el movimiento, la energía potencial alcanzó su máximo en los puntos más altos de la trayectoria (θ=±0,26rad), como resultado de la constante transferencia de energía entre las formas cinética y potencial. Estos resultados experimentales respaldan el comportamiento teórico de un péndulo simple ideal sin fricción, confirmando la validez del modelo utilizado. La conservación de la energía total del sistema durante el movimiento del péndulo confirma la ausencia de pérdida de energía, característica fundamental de un sistema ideal. Y así verificando que la variación sinusoidal de las energías cinética y potencial se explica por el principio de conservación de la energía mecánica.

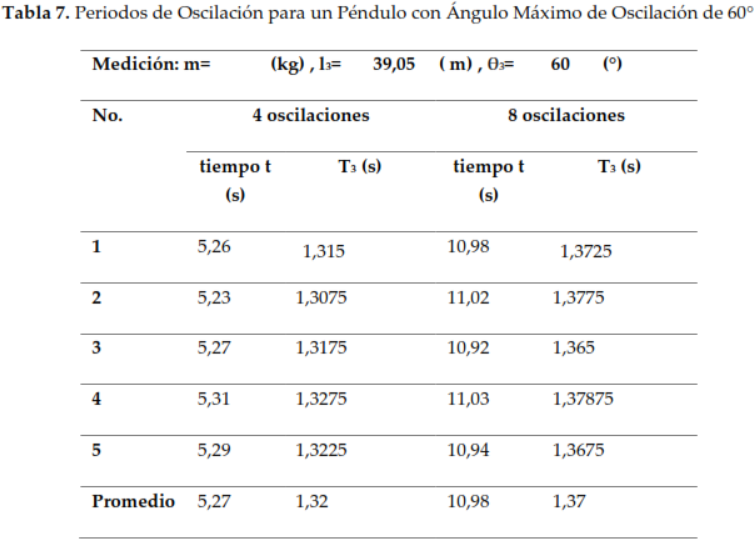
Mediante esta experiencia, se evidencia que, aunque el péndulo simple sirve como un ejemplo clásico de un sistema que exhibe movimiento armónico simple (MAS), esta descripción es una aproximación tal que sin(θ) ≈ θ, misma que solo resulta válida para ángulos pequeños, específicamente aquellos que no superan los 15°. Esto se debe a que solo en estos casos se puede aplicar la equivalencia matemática que define al MAS. Para ángulos más grandes, como el de 60° utilizado en este experimento, el sistema exhibe comportamientos más complejos que no pueden ser capturados por la ecuación del MAS. Esto se debe a que la aproximación de ángulos pequeños ya no es válida y el sistema comienza a desviarse del comportamiento idealizado del MAS

Actividad 4:

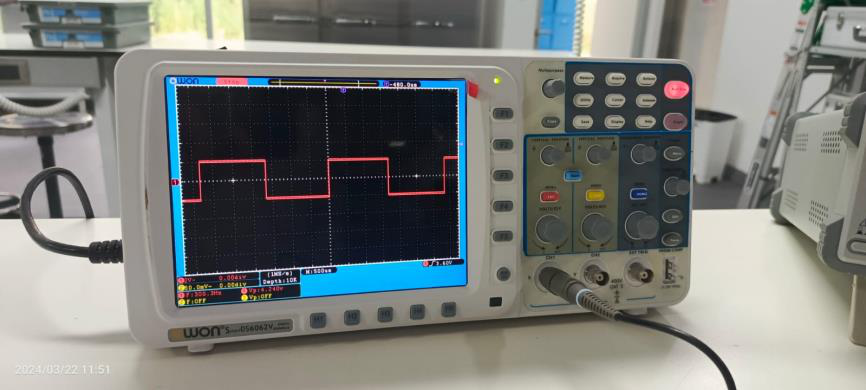
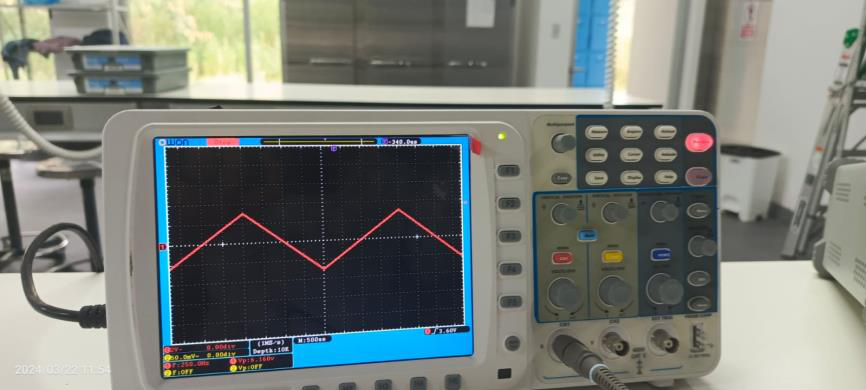
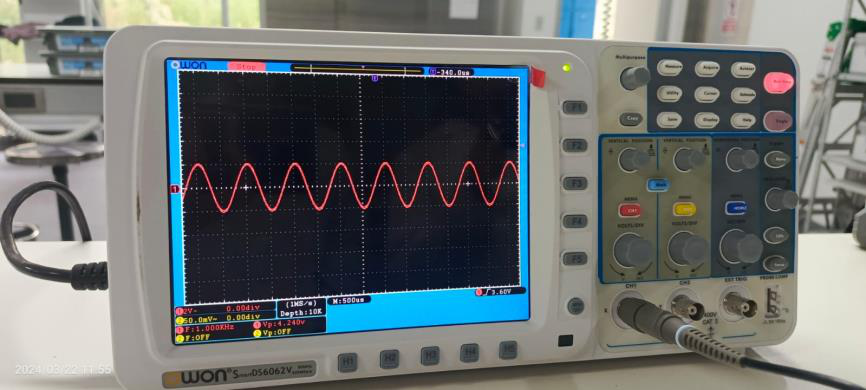
En esta actividad, se utilizó al osciloscopio para producir y analizar tres tipos distintos de ondas: cuadrada, triangular y sinusoidal, primero, se generó una onda cuadrada con una frecuencia de 300 Hz y una amplitud pico de 2V. A partir de estos parámetros, se calculó el período de la onda cuadrada como el inverso de la frecuencia, resultando en un valor de aproximadamente 3.33 ms. Posteriormente, se produjo una onda triangular con un período de 4 ms y una amplitud pico de 3V. Con base en estas especificaciones, se calculó la frecuencia de la onda triangular como el inverso del período, obteniendo un valor de 250 Hz. Finalmente, se generó una onda sinusoidal con una frecuencia de 1 kHz y una amplitud pico de 2V. A partir de estos datos, se calculó el período de la onda sinusoidal como el inverso de la frecuencia, resultando en un valor de 1 ms. Las gráficas de las ondas generadas se presentan en las Figuras 11, 12 y 13.

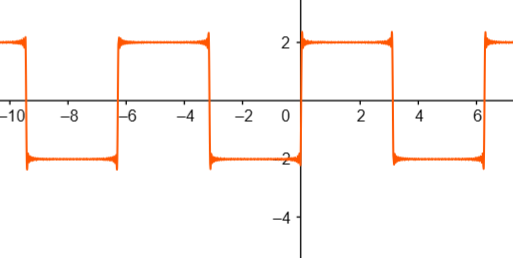
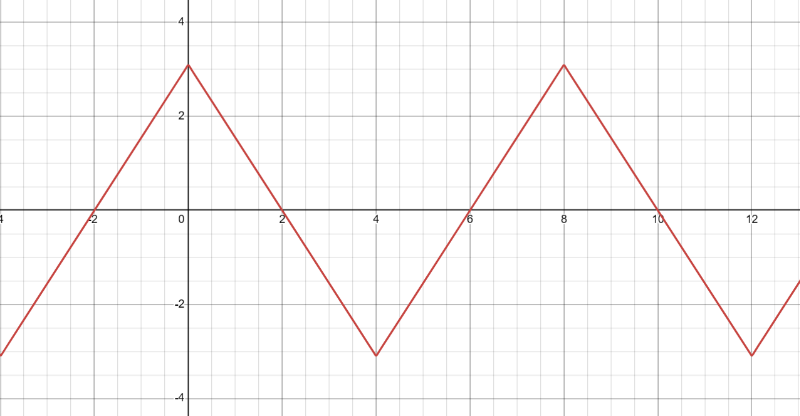
El objetivo de esta actividad es que los estudiantes aprendan a utilizar correctamente los instrumentos y comprendan los datos que cada dispositivo proporciona. En este caso específico, los resultados obtenidos tras graficar las ondas permitieron observar la capacidad del generador de funciones para producir diferentes tipos de ondas con diversas frecuencias y amplitudes con un alto nivel de precisión. Esto facilita la realización de simulaciones y cálculos teóricos previos, permitiendo una mejor comparación y contraste junto con el refuerzo de los conceptos teóricos.

Discusión

¿Qué pasaría si al resorte de la actividad 2 se aplica un impulso que genera una velocidad inicial diferente de cero?
Si a un resorte se le aplica un impulso que genera una velocidad inicial diferente de cero, esto cambiará las condiciones iniciales del movimiento armónico simple (MAS). El resorte comenzará a oscilar con una amplitud que depende de la energía total del sistema, que ahora incluye tanto la energía potencial elástica como la energía cinética inicial debida al impulso aplicado. [1]
En el péndulo elástico, ¿Qué pasa con la frecuencia angular al aumentar la masa?
En un péndulo elástico, la frecuencia angular no depende de la masa. Esto se debe a que, en el MAS, la frecuencia angular es una función de la constante del resorte (k) y la masa (m), dada por la relación.

Por lo tanto, al aumentar la masa, la frecuencia angular disminuirá, ya que están inversamente relacionadas. [2-3]
En el péndulo simple, ¿Qué pasa con la frecuencia angular al aumentar la longitud?
En un péndulo simple, la frecuencia angular está dada por:

Donde (g) es la aceleración debido a la gravedad y (L) es la longitud del péndulo. Al aumentar la longitud (L), la frecuencia angular disminuirá, ya que la frecuencia angular es inversamente proporcional a la raíz cuadrada de la longitud del péndulo. [4-5]

Conclusiones

La comprensión de los principios fundamentales que rigen los movimientos armónicos simples (MAS) ha mejorado como resultado de la práctica en el laboratorio de oscilaciones. Experimentos meticulosos con un péndulo y un sistema de masa-resorte han demostrado la relación inversa entre la frecuencia de oscilación y la amplitud. También se ha demostrado que la fase inicial tiene un impacto en la posición de inicio del movimiento oscilatorio. Estos hallazgos no solo respaldan las teorías existentes, sino que también brindan una base experimental útil para investigaciones futuras en sistemas oscilatorios de mayor complejidad. Estos resultados son significativos debido a su capacidad para predecir el comportamiento de los osciladores en una variedad de aplicaciones prácticas, como relojes e instrumentos musicales. Esto demuestra la importancia del MAS en la vida real.

Referencias